
#MEASURE ANGLES WITH A PROTRACTOR HOW TO#
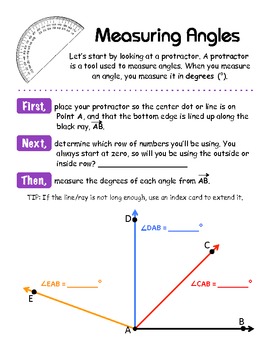
Then Cathy gave them the challenge of figuring out how to use the protractors and writing directions that someone else could follow. “It may be helpful to use a right angle as a reference,” she suggested, “since you already know a right angle is ninety degrees.”Īfter a while, Cathy called the class to attention and asked the students to share what they had noticed. When Cathy distributed protractors to her class in San Jose, California, she told the students, “The protractor is a useful tool for both measuring angles and drawing angles of specific sizes.” She asked the students to work in pairs and explore the protractors. Often they don’t see the need for the tool, so Cathy does not introduce protractors until after the students have had concrete experiences measuring angles several ways. That is, they should all experience challenging, intellectually worthwhile and coherently-structured mathematics.From her past experiences teaching middle school students about angles, Cathy Humphreys knew that students often have difficulty learning how to use protractors. Levels of mathematical integrity, then the case for acceleration would be seen for the falsehood it is. Additionally, tasks such as those described above illuminate the debate concerning the so-called gifted and talented - if all exercises were as purposeful, and exhibited comparable It is my conjecture that there really is, despite Woodhead's pre-resignation rants and selective use of data toĬon ministers otherwise, no justification for the misery English schools inflict on their pupils through their indiscriminate use of setting and its predetermination of minimal educational attainment for so many.

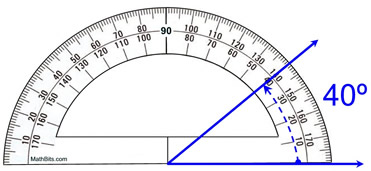
In so doing, I hope I have gone part-way to convincing colleagues that such tasks are accessible at a range of levels and, therefore, appropriate for mixed ability working. In this article I have attempted to establish a principle of worthwhile mathematical activity for all pupils. Ironically, the way in which the task was presented meant that no measurement was needed - pupils could simply read off the required angle from the scale. That is, pupils were givenĪlmost one hundred and fifty opportunities to repeat the same task. The exercise itself was repeated twice more over the page. This was followed by almost fifty requests for them to repeat the process. The first question invited them to measure, say, angle $\angle AOB$. In this particular lesson pupils were working from a text which contained, on one page, a picture similar to that in figure 1, albeit with a greater number of labels. Within a more meaningful and mathematically coherent activity. Also, I wanted a means by which practice could be embedded During the lesson, as pupils were working their way through one of the most turgid exercises imaginable, I began thinking about how such work might be made more relevant to such classes - that is classes where the evidence shows that a substantial number of children can already manage, with competence, the skill being taught. The teacher was aware of this but felt she hadn't the resources or the authority to do somethingĭifferent. Admittedly she was following the scheme of work specified by her head of department, but it saddened me to see so many children doing something which they could clearly already do. I was observing a lesson recently in which the teacher was showing her year seven class how to use a protractor.


 0 kommentar(er)
0 kommentar(er)
